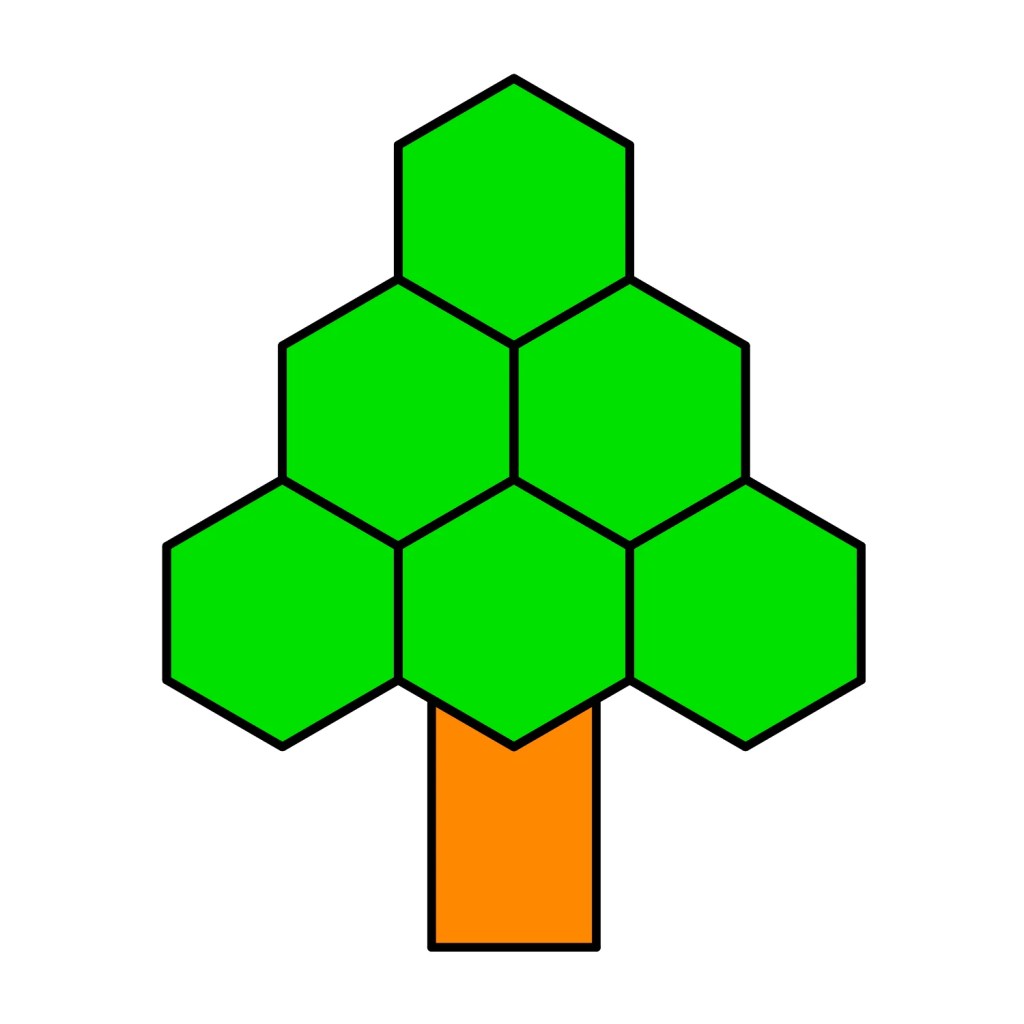
Fill each regular hexagon in the Christmas tree with a different prime number. Each side of the triangle the tree makes must add to the same sum and each line’s total should be as small as possible.

Note that, by convention, 1 isn’t a prime number.

This puzzle was published on the New Scientist.

Solution

The minimum total is 33 (= 3 + 13 + 17 = 3 + 19 + 11 = 11 + 5 + 17).

Note that the triangle of values can be rotated/reflected to give equivalent arrangements.