ENIGMATH's header.

Puzzle #29

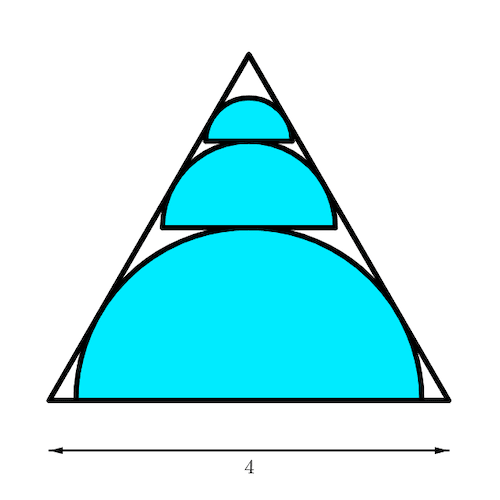
An equilateral triangle has three semicircles inside it that are tangent to its transversal sides. A horizontal double arrow that represents the length of the base of the equilateral triangle is labeled/labelled four.

An equilateral triangle with side length 4 has three semicircles inside it that are tangent to its transversal sides. The semicircles are the first three terms of an infinite geometric sequence.

What is the sum of the areas of all the semicircles in the sequence?

Solution

Let r be the radius of the semicircle in the bottom of the equilateral triangle. As the semicircles are tangent to the transversal sides of the triangle, we get a 30-60-90 triangle.

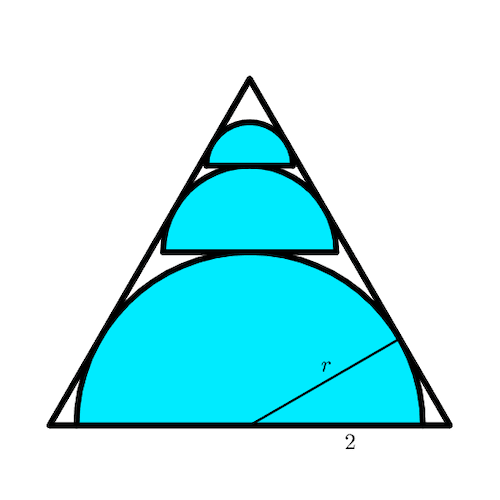
An equilateral triangle with side length four has three semicircles inside it that are tangent to its transversal sides. A right/right-angled triangle is on the bottom right of the equilateral triangle where one of the sides is labeled/labelled r, the radius of the bottom semicircle, and the hypotenuse is labeled/labelled two.

Then, the side lengths of the 30-60-90 triangle are

An equilateral triangle with side length four has three semicircles inside it that are tangent to its transversal sides. A right/right-angled triangle is on the bottom right of the equilateral triangle where two sides are labeled/labelled square root of three, the radius of the bottom semicircle, and one, and the hypotenuse is labeled/labelled two.

Then,

r=\sqrt{3}

So, the area of the bottom semicircle is

\frac{\pi \left( \sqrt{3} \right)^2}{2}

\frac{3\pi}{2}

The height of the equilateral triangle is

2 \sqrt{3}

As the radius of the bottom semicircle is

\sqrt{3}

the middle semicircle is tangent to an equilateral triangle similar to the original one, with side length 2.

The radius of the middle semicircle is

\frac{\sqrt{3}}{2}

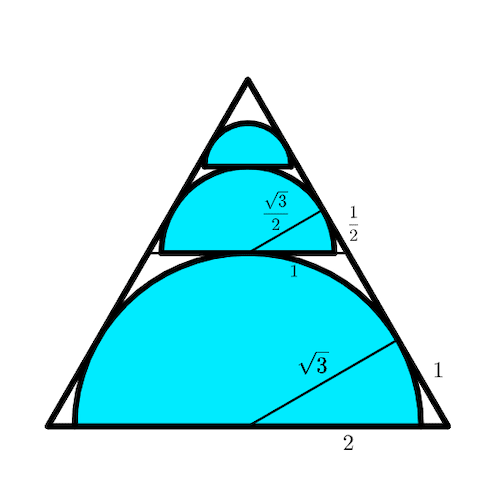
An equilateral triangle with side length four has three semicircles inside it that are tangent to its transversal sides. A right/right-angled triangle is on the bottom right of the equilateral triangle where two sides are labeled/labelled square root of three, the radius of the bottom semicircle, and one, and the hypotenuse is labeled/labelled two. A right/right-angled triangle is on the bottom right of the middle semicircle where two sides are labeled/labelled square root of three over two, the radius of the middle semicircle, and one half, and the hypotenuse is labeled/labelled one.

So, the area of the middle semicircle is

\frac{\pi \left( \frac{\sqrt{3}}{2} \right)^2}{2}

\frac{3\pi}{8}

Similarly, the top semicircle has radius

\frac{\sqrt{3}}{4}

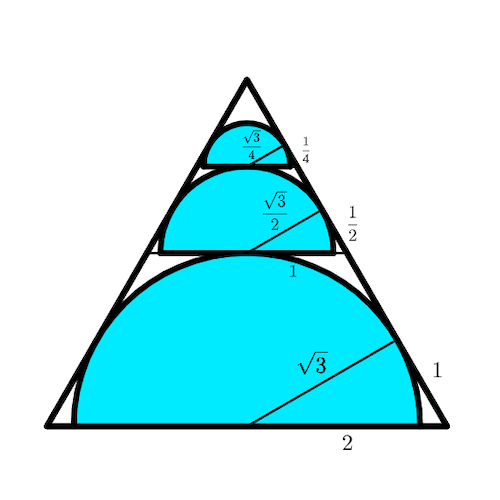
An equilateral triangle with side length four has three semicircles inside it that are tangent to its transversal sides. A right/right-angled triangle is on the bottom right of the equilateral triangle where two sides are labeled/labelled square root of three, the radius of the bottom semicircle, and one, and the hypotenuse is labeled/labelled two. A right/right-angled triangle is on the bottom right of the middle semicircle where two sides are labeled/labelled square root of three over two, the radius of the middle semicircle, and one half, and the hypotenuse is labeled/labelled one. A right/right-angled triangle is on the bottom right of the middle semicircle where two sides are labeled/labelled square root of three over four, the radius of the top semicircle, and one quarter.

and its area is

\frac{3\pi}{32}

The area of the semicircles forms a geometric sequence with common ratio

\frac{\frac{3\pi}{8}}{\frac{3\pi}{2}}

\frac{1}{4}

The sum of the semicircle’s areas is

\displaystyle \sum_{n=1}^\infty \frac{\pi \left( \frac{\sqrt{3}}{2^{n-1}} \right)^2}{2}

\displaystyle \sum_{n=1}^\infty \frac{\frac{3\pi}{2^{2n-2}}}{2}

\displaystyle \sum_{n=1}^\infty \frac{3\pi}{2^{2n-1}}

\displaystyle 3\pi \sum_{n=1}^\infty \frac{1}{2^{2n-1}}

We have the infinite geometric sequence

\frac{1}{2^{2n-1}}

The sum of an infinite geometric sequence is given by

\frac{a}{1-r}

where a is the first term and r is the ratio of the sequence.

Then, the sum is

\frac{\frac{1}{2}}{1-\frac{1}{4}}

\frac{\frac{1}{2}}{\frac{3}{4}}

\frac{2}{3}

So, the area of all the semicircles of the infinite sequence is

\displaystyle 3\pi \sum_{n=1}^\infty \frac{1}{2^{2n-1}}

3\pi \times \frac{2}{3}

2\pi

Share this post

Don’t miss any post from ENIGMATH

Subscribe to get the latest posts sent to your email.

Leave a comment

Trending

Don’t miss any post from ENIGMATH

Subscribe to get the latest posts sent to your email.

Continue reading