Puzzle #28

December 30, 2025

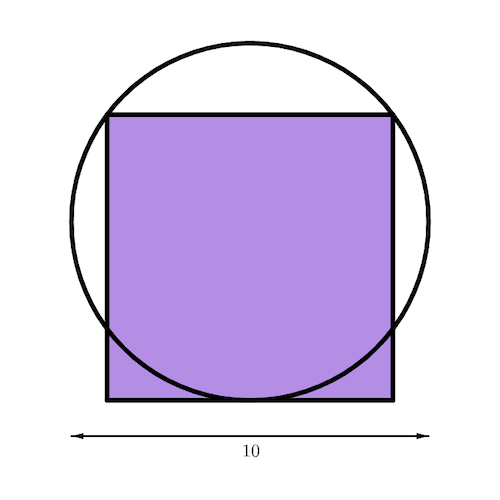
A circle has diameter 10.

What is the area of the square?

Solution

As the circle has diameter 10, its radius is 5.

Let x be the square’s side length.

Consider the right/right-angled triangle below.

Its hypotenuse is 5, the radius of the circle. The horizontal side is half of the square’s side length and its vertical side measures x − 5.

Using the Pythagorean/Pythagoras’ theorem:

$5^2=\left(x-5\right)^2+\left(\frac{x}{2}\right)^2$

$25=x^2-10x+25+\frac{x^2}{4}$

$0=x^2-10x+\frac{x^2}{4}$

$0=4x^2-40x+x^2$

$5x^2-40x=0$

$5x\left(x-8\right)=0$

$x=0, \, x=8$

Then square’s length is

$x=8$

So, the area of the square is

$8^2$

$64$

Share this post

Subscribe to get the latest posts sent to your email.

Wag