Puzzle #27

December 22, 2025

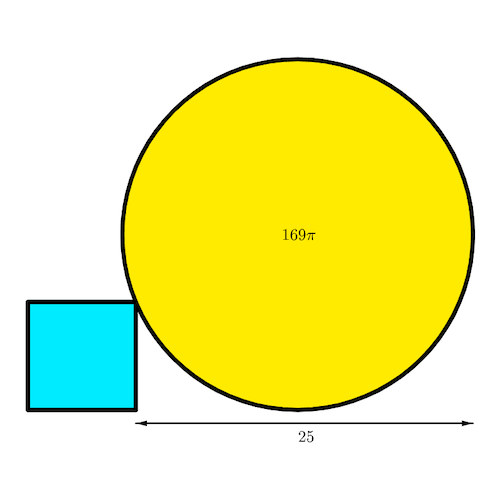
A circle with area 169π is aligned with the square’s base.

What is the area of the square?

Solution

As the area of the circle is 169π, its radius is 13.

Let x be the square’s side length.

Consider the right-angled/right triangle below. Its hypotenuse is 13, its base’s length is 25 − 13 = 12 and its height is 13 − x:

Using the Pythagorean /Pythagoras’ theorem:

$13^2=12^2+\left(13-x\right)^2$

$169=144+169-26x+x^2$

$x^2-26x+144=0$

$\left(x-8\right)\left(x-18\right)=0$

$x=8, \, x=18$

As the square’s length is less than the radius, then

$x=8$

So, the area of the square is

$8^2$

$64$

Share this post

Subscribe to get the latest posts sent to your email.

Wag